Yeni İçerik Fikirleri

Uzun bir süredir yeni yazı yazmıyordum. Yeniden yazmaya başladım. Bundan sonra SPSS ile ilgili birkaç yazı ekledikten sonra veri madenciliği, R , SQL, Orange, Weka gibi konular üzerine yazmayı düşünüyorum. Eğer varsa sizlerin önerilerini de duymayı çok isterim. (Yorumlarla yada doğrudan bana mail atarak önerilerinizi bana ulaştırabilirsiniz.)

Virgülle Ayrılmış Veri Setini(CSV) SPSS ile Açma

Virgülle ayrılmış veri(Comma Seperated Values - CSV) formatı veri analizi çalışmalarında en yaygın olarak kullanılan dosya tipidir. Bu kadar yaygın olmasının sebebi neredeyse mevcut bütün veri analizi programları tarafından desteklenmesidir. Ayrıca farklı programlar arasında da kolay veri aktarımını sağlar. Örneğin veri tabanlarından dışarı veri aktarma aşamasında(exporting) yada açık kaynak kodlu R, Weka, Orange gibi programlardan SPSS, Excel gibi daha yaygın programlara veri aktarımında kullanılabilir.. Bu bölümde bu dosya tipinin SPSS'e nasıl aktarılacağına bakacağız. Örnek dosyayı buradan indirebilirsiniz.

Bu tip dosya tipleri "Virgülle Ayrılmış Veri" olarak çağrılsa da aslında genellikle değişkenler noktalı virgülle(;) ile ayrılır. Bunun sebebi ondalıklı sayıların virgüllü kısmının programlar tarafından ayrı bir değişken olarak algılanmasını engellemektir.

SPSS' de bu tip dosyaları açarken "File > Open > Data" bölümünden yada doğrudan ilgili dosyayı SPSS'in data editörünün üstüne sürükleyerek SPSS'in text okuma sihirbazını çalıştırabilirsiniz.

Bundan sonra açılan pencerede SPSS bilgisayarınızdan ilgili dosyayı bulmanız gerekiyor. Aşağıdaki bölümde gösterilen dosya tiplerini değiştirmeyi unutmayın. Aksi takdirde SPSS sadece kendi dosyalarını(.sav uzantılı) 
gösterecektir.

Dosya seçme işlemi başladıktan sonra "Text Import Wizard" çalışacaktır.

Bu ilk pencerede SPSS size bu dosya tipinin daha önce tanımlanmış bir dosya tipiyle uyuşup uyuşmadığını bize sorar. Bu örnekte tanımlı olmadığı için "No" yu seçip devam ediyoruz.

Bu pencerenin ilk kısmında verilerin belirli bir ayraçlamı yoksa bir hizaya göre mi ayrıldığını soruyor. Bu veri seti bir ayraçla(noktalı virgül) ayrıldığı için "Delimited" seçeneği seçilir. İkinci bölümde ise veri setinin en üst satırında veri isimlerinin olup olmadığını soruyor. Bu veri setinde veri isimleri en üst satırda olduğu için "Yes" i seçip ilerleyebilirsiniz.

Bir önceki pencerede veri isimleri en üst satırda olduğu için verilerin başladığı satır numarası kendiliğinden 2 olarak ayarlanıyor. Bu pencerede aynı zamanda örneklemede yapılabilir. Verilerin tamamını, ilk x tane veriyi yada rastgele olarak belirli bir yüzdesini seçebilirsiniz.

Bu bölümde ise verilerin ne tür bir ayraç ile ayrıldığı seçilir. Burada "Semicolon(noktalı virgül)" seçeneğini işaretlendiğinde verilerin bir düzene girdiği görülebilir.

Bu bölümde ise veri isimleri ve tipleri düzenlenebilir. Bu veri setinde bütün değişkenler nümerik olduğu için "Numeric" seçeneği seçilir.

Bu pencerenin üst bölümünde SPSS "bu dosya tipini ilerde kullanmak için kaydetmek ister misiniz?" diye soruyor. İsteğe göre kaydelilebilir. Ben kaydetmedim. "Finish" tuşuna basarak Text Import Wizard sonlandırılır. Veri seti aşağıdaki gibi olacaktır.

Bunun ardından ilgili analizler veri setine uygulanabilir.

SPSS:Lİneer Regresyon

Regresyon analizi, bir yada birden daha fazla bağımsız değişkenin, bağımlı bir değişkenle arasındaki ilişkiyi matematiksel bir denklem olarak orataya koymak için kullanılır. Burada;
Y : Bağımlı değişken
X: Bağımsız değişken
B: Katsayılar
E: Artıklar
olmak üzere Y=B0+B1+B2X2+…+BkXk+ei şeklinde bir denklem elde edilir. Böylece "şu "X" verisi için "Y" değeri bu olacaktır." şeklinde tahminler yapılabilir. ( Örnekte incelenecek veri setini buradan indirebilirsiniz... )

Burada "y"(Vücut ağırlığı)" değişkeni bağımlı veri, "x"(Vucudun farklı bölümlerinin ölçüleri) değişkenleri ise bağımsız verilerdir.
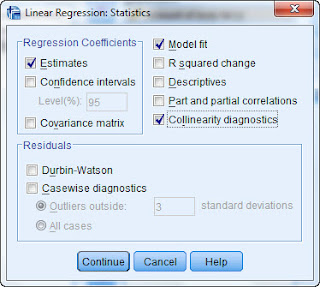
SPSS' de " Analyze > Regression > Linear "

Bu seçimler yapıldıktan sonra sonuçlar aşağıdaki gibi olacaktır.

Bu tablodaki "Adjusted R Square" değeri oluşturulan denklemin tahmin gücünü göstermektedir. Bu modelin tahmin gücü %99.9' dur.

 Bu tabloda "Sig." değer 0.000<0.05 olduğu için oluşturulan modelin anlamlı bir model olduğu yorumu yapılabilir.

Bu tablodan modelin matematiksel hali oluşturulabilir ve katsayıların bağımlı değişken üzerinde anlamlı bir etkiye sahip olup olmadıkları yorumu yapılabilir. Burada "Midarm Circumference" değişkeninin "Sig." değeri 0.170>0.05 olduğu için bu değişkenin bağımlı değişken üzerinde anlamlı bir etkisi yoktur. Böyle bir durumda "Stepwise Regression" yöntemi kullanılır.

SPSS:Correlation

Korelasyon katsayısı, iki değişkenin arasındaki lineer ilişkinin yönünü ve miktarını ifade eden bir niceliktir. -1 ile +1 arasında değer alır. "r" korelasyon katsayısı olmak üzere;

Bivariate: İki değişken arasındaki korelasyon katsayısını bulmak için kullanılır.
Partial: İncelenen iki değişkenle ilişkisi olduğu düşünülen bir yada birden fazla değişkenin göz önünde bulundurularak iligili iki değişkenin arasındaki korelasyon katsayısını hesaplamak için kullanılır.
(Örnekte incelenecek veri setini buradan indirebilirsiniz.)

y=Body Fat     x1=Triceps skinfold thickness     x2=Thigh circumference     x3=Midarm circumference
Bu veris setinde "y" değişkeni bağımlı değişken ve x1, x2, x3 değişkenleri ise bağımsız değişkenlerdir. Bunlar kişilere ait vucut ağırlıkları(y) ve bu kişilere ait farklı vucut ölçüleridir(x1,x2,x3). İlk olarak bağımsız değişkenler arasındaki korelasyon katsayılarını inceleyelim.

SPSS' de " Analyze > Correlation > Bivariate "

 Bu diyalog kutusunda hangi değişkenlerin aralarındaki korelasyon katsayıları hesaplanmak isteniyorsa o değişkenler "Variables" bölümüne atılır. "Options" seçeneğinden ise isteğe bağlı olarak bazı tanımlayıcı istatistikler hesaplatılabilir. "Correlation Coefficients" bölümü ile ilgili; eğer araştırılmak istenen değişkenler normal dağılım gösteriyorsa "Pearson" seçeneği, normal dağılım göstermiyorsa "Spearman" seçeneği seçilir. (Normallik testi ile ilgili ayrıntılı bilgiyi buradan bulabilirsiniz. )
Bu seçimler yapıldıktan sonra sonuçlar aşağıdakilere benzer şekilde olacaktır.

Tabloda görüldüğü gibi "Triceps skinfold thickness" ve "Midarm circumference" değişkenlerinin arsında pozitif yönlü, orta seviye (neredeyse güçlü) bir korelasyon(r = 0.878) vardır. Diğer ikililer arasındaki korelasyonların zayıf olduğu görülür.
Şimdi "Body Fat" değişkenini göz önünde bulundurarak aynı değişkenler arasındaki korelasyonu(kısmi korelasyon) hesaplayalım.
SPSS' de " Analyze > Correlation > Partial "

Bu seçimler yapıldıktan sonra sonuçlar aşağıdaki gibi olacaktır. (Tabloyu büyütmek için üzerine tıklayınız.)

"Body fat" değişkeni göz önünde bulundurulduğunda "Triceps skinfold thickness" ve "Thigh circumference"değişkenleri arasında negatif yönlü güçlü bir korelasyonun olduğu görülür( r = -0.994). Halbuki ilk tabloda bu iki değişken arasındaki korelasyon zayıf bir korelasyodu.

SPSS:MANOVA

MANOVA, birden fazla bağımlı değişkenin bulunduğu deneylerde varyans analizi yapmak için kullanılan bir tekniktir. Univariate ANOVA' dan tek farkı, birden fazla bağımlı değişkenin olmasıdır. Ayrıca "Multivariate", yine birden fazla bağımlı değişkenin bulunduğu Çoklu Regresyon Analizinde de kullanılır. Gerekli varsayımlar yine normal dağılım ve homojen varyans varsayımlarıdır. (Hipotezlerin kurulması ve ortalamaların karşılaştırılmasıyla ilgili ayrıntılı bilgiyi Univariate ANOVA bölümünden bulabilirsiniz.)

Bu veri seti bir plastik fabrikasının ürettiği ürünlerle ilgilidir. Burada "Resistance(Dayanıklılık)", "Gloss(Parlaklık)" ve "Opacity(Saydamlık)" değişkenleri bağımlı değişkenlerdir. Faktörler ise "Extrusion_rate" ve "Additive" sütunlarıdır. Burada her faktörün "0" ve "1" olmak üzere iki düzeyi vardır. Dolayısıyla "Post Hoc" testleri uygulanamaz.(Post Hoc testleri için en az üç düzey gerekir.)

SPSS' de " Analyze > General Linear Model > Multivariate "

Burada, eğer fakör düzeyleri rastgele eşleştirilmiş olsaydı ilgili faktör yada faktörler "Random Factor" bölümüne atılırdı.Eğer faktörlerin değişkenleri kantitativ(nicel, sayısal) olsaydı bu sefer ilgili faktör yada faktörler "Covariate" bölümüne atılırdı.

 "Model" bölümünde, hangi faktörlerin yada bu faktörlerin etkileşimlerinin, bağımlı değişken üzerinde etkisi olup olmadığı araştırılıyorsa onlar seçilir. "Full factorial" bölümü işaretli olduğu zaman, SPSS tüm faktörleri ve bu faktörlerin olası bütün etkileşimlerini modele koyar. "Custom" bölümünden ise isteğe göre bir model oluşturulabilir. "Sum of squares" bölümünde, eğer kayıp gözlemler varsa "Type IV" , eğer kayıp gözlem yoksa "Type III" seçilir.

"Options" bölümünde, istenilen faktör yada faktör etkileşimlerinin marjinal ortalamaları hesaplatılabilir ve testin güvenilirliği belirlenir. Ayrıca gerekli varsayımlardan birisi olan varyansların homojenliği testi için "Homogeneity tests" bölümü seçilir. Bu seçimler yapıldıktan sonra sonuçlar aşağıdakilere benzer şekilde olacaktır.

Homojenlik testinde bütün bağımlı değişkenlerin "Sig." değerleri 0.05 den büyük olduğu için "%95 güvenle tüm bağımlı değişkenler için varyanslar homojendir." yorumu yapılabilir.

MANOVA tablosu(Multivariate Tests) tablosu incelenciğinde birden fazla test olduğu görülür. Bu testlerden genellikle "Pillai' s Trace" ve "Wilks' Lambda" testleri dikkate alınır. Faktörlerin "Sig." değerleri inceleniğinde, "Extrusion_rate" ve "Additive" faktörlerinin "Sig." değerlerinin 0.05 den küçük oldudğu görülür. Yani " %95 güvenle, "Extrusion_rate" ve "Additive" faktörlerinin bağımlı değişkenler üzerinde istatistiksel olarak anlamlı bir etkisi vardır." yorumu yapılabilir. "Extrusion_rate*Additive" etkileşiminin ise bağımlı değişkenler üzerinde bir etkisi yoktur.("Sig."=0.302>0.05)

Ayrıca SPSS bütün bağımlı değişkenler için ayrı ayrı Univariate ANOVA testini de yapar. Böylece bütün faktör ve faktör etkileşimlerinin, bağımlı değişkenler üzerindeki marjinal etkileri incelenebilir.

SPSS:Univariate ANOVA

Univariate ANOVA, iki yada ikiden daha fazla faktöre ait değişkenlerin ortalamalarını karşılaştırmak için kullanıllır. One-Way ANOVA' dan farkı iki yada ikiden daha fazla faktörün olmasıdır. ANOVA testiyle hangi faktörün bağımlı değişken üzerinde anlamlı bir etkisi olup olmadığı tespit edilir. Post Hoc testleriyle ise eğer faktör düzeyleri arasında bir farklılık var ise bu faklılığın hangi düzeyler arasında olduğu bulunur. Varsamyımlar One-Way ANOVA ile aynıdır. Nomallik ve varyansların homojenliği. (Örnekte incelencek veri setini buradan indirebilirsiniz.)

Burada fakörler "Shelf" ve "Store" sütunları, bağımlı değişken ise "Sales" sütunudur. Bu veri seti, bir süpermarketin iki farklı şubesindeki(Store), üç farklı raftaki(Shelf) ürünlerin satış miktarını(Sales) gösteriyor. Teste başlamadan önce normallik testi yapılmalıdır. Burada veriler normal dağılımlıdır. Ortalamaları karşılaştırmak için öncelikle hipotezler kurulmalıdır.

H0: %95 güvenle, faktör düzeylerinin ortalamaları arasında istatistiksel olarak anlamlı bir farklılk yoktur.
H1: %95 güvenle, faktör düzeylerinin ortalamaları arasında istatistiksel olarak anlamlı bir farklılk vardır

SPSS' de " Analyze > General Linear Models > Univariate " (Resimleri büyütmek için üzerine tıklayın...)

Burada, eğer fakör düzeyleri rastgele eşleştirilmiş olsaydı ilgili faktör yada faktörler "Random Factor" bölümüne atılırdı.Eğer faktörlerin değişkenleri kantitativ(nicel, sayısal) olsaydı bu sefer ilgili faktör yada faktörler "Covariate" bölümüne atılırdı.

"Model" bölümünde, hangi faktörlerin yada bu faktörlerin etkileşimlerinin, bağımlı değişken üzerinde etkisi olup olmadığı araştırılıyorsa onlar seçilir. "Full factorial" bölümü işaretli olduğu zaman, SPSS tüm faktörleri ve bu faktörlerin olası bütün etkileşimlerini modele koyar. "Custom" bölümünden ise isteğe göre bir model oluşturulabilir.

"Post Hoc" bölümünde, faktör düzeyleri arasındaki olası farklılıklara karşın, bu farklılıkların hangi düzeyler arasında olduğunu tespit etmek için ilgili testler seçilir. Varyansların homojen olması durumunda genellikle
"Tukey" testi tercih edilir. Varyansların homojen olmaması durumunda ise genellikle " Tamhane' s T2" testi tercih edilir.

"Options" bölümünde, testin güvenilirliği belirlenir, homojenlik testi seçilir ve istenilen faktörler için tanımlayıcı istatistikler hesaplatılabilir. Bu seçimler yapıldıktan sonra sonuçla aşağıdaki gibi olacaktır.

"Sig" değeri 0.315 > 0.05 olduğu için faktörlerin varyansları homojendir.

Bu tabloda "Store" ve "Store*Shelf" faktörlerinin "Sig" değerleri 0.550 > 0.05 ve 0.467 > 0.05 olduğu için bu faktörler için H0 hipotezleri kabul edilir. Yani " %95 güvenle, bu faktör düzeylerinin ortalamaları arasında, istatistiksel olarak anlamlı bir farklılık yoktur." denilebilir. Dolayısıyla bu faktörlerin satışlar üzerinde anlamlı bir etkisi yoktur. Ancak "Shelf" fakörünün "Sig" değeri 0.001 < 0.05 olduğu için H0 hipotezi reddedilir. Yani "%95 güvenle,"Shelf" faktörünün düzeylerinin ortalamaları arasında, istatistiksel olarak anlamlı bir farklılık vardır." denilebilir. Bu farklılıkların hangi düzeyler arasında olduğunu tespit etmek için "Tukey" testinin sonuçları incelenmelidir.

Bu tabloda faktör düzeyleri ve bu faktör düzeylerinin ortalamaları arasındaki farklar sayısal olarak verilmiştir. Tablodaki bu sayısal farklılıkların yanındaki yıldız(*) işereti, bu farklılıkların anlamlı bir farklılık olduğunu göstermektedir. Dolayısıla tablo incelendiğinde 3. faktör düzyeinin ortalamasının diğer iki düzeyin ortalamasından farklı olduğu görülür.

Son olarak "Shelf" faktörünün ortalama tablosu incelendiğinde, 3.düzeyin(3. raf çeşidinin) ortalamasının diğerlerinden daha büyük olduğu görülür. Yani "3. raftaki satışlar diğerlerinden daha fazladır." yorumu yapılabilir.

SPSS:One Way ANOVA(Tek Yönlü Varyans Analizi)

Tek yönlü varyans analizi, bir faktör çatısı altında, iki yada ikiden daha fazla bağımsız grubun ortalamalarını karşılaştırmak için kullanılır. Tek yönlü varyans analizinde iki temel varsayım vardır. Her grup normal dağılımlıdır ve göreceli olarak grupların varyansları homojendir. (Örnekte kullanılacak veri setini buradan indirebilirsiniz...)

Bu veri seti, bir yemek şirketine ait ürün çeşitlerinin satış miktarlarını göstermektedir. Burada "sales" değişkeni(Bağımlı değişken) satış miktarını, "design"(Faktör) değişkeni ise ürün çeşitlerini ifade etmektedir. Burada ürün çeşitlerinin satış miktarları birbirinden bağımsızdır ve normal dağılıma sahiptir. (Normallik testinin nasıl yapıldığına buradan bakabilirsiniz.) Dolayısıyla bu grupların satış miktarlarının ortalamalarını karşılaştırmak için en uygun test tek yönlü varyans analizi olur. Öncelikle hipotezler kurulmalıdır.

Varyansların homojenliği testi için hipotezler;
H0: %95 güvenle grup varyanslar homojendir.
H1: %95 güvenle grup varyansları homojen değildir.

Tek yönlü varyans analizi için hipotezler;
H0:  %95 güvenle, grupların ortalamaları arasında istatistiksel olarak anlamlı bir farklılık yoktur.
H1:%95 güvenle, grupların ortalamaları arasında istatistiksel olarak anlamlı bir farklılık vardır.

SPSS' de "Analyze > Compare Means > One-Way ANOVA"

Burada homojenlik testi için, "Options" bölümünden "Homogeneity of variance test" bölümü seçilir. İsteğe bağlı olarak "Descriptives" seçeneği işaretlenerek tanımlayıcı istatistikler de hesaplatılabilir.

"Post Hoc" bölümünden ise varyansın homojen olup olmamasına göre yapılması istenen test yada testler seçilir.

Burada varyansların homojen olması halinde(Equal variances Assumed) yapılacak testlerden, genellikle "Tukey" testi tercih edilir. Veri sayısının az olduğu zamanlarda "Bonferroni" testi de seçilebilir. Varyansların homojen olmaması halinde(Equal Variances Not Assumed) yapılacak testlerden ise genellikle "Tamhane's T2" testi tercih edilir.
Bu seçimler yapıldıtan sonra sonuçlar aşağıdaki gibi olacaktır.

Burada "Sig." değeri 0.729>0.05 olduğu için homojenlik testi için olan H0 hipotezi kabul edilir. Yani " %95 güvenle grupların varyansları homojendir." denilebilir.

ANOVA tablosu incelendiğinde, "Sig." değeri 0.000<0.05 olduğu için tek yönlü varyans analizi için olan H0 hipotezi reddedilir. Yani " %95 güvenle, grupların ortalamaları arasında istatistiksel olarak anlamlı bir farklılık vardır." denilebilir.
Hangi grupların ortalamaları arasında farklılıklar olduğunu görmek için bir sonraki tablo incelenir. (Tabloyu büyütmek için üzerine tıklayınız.)

Burada grupların varyansları homojen olduğu için "Tukey" testi incelenir(Eğer homojen olmasaydı "Tamhane" testi incelenirdi). Bu tabloda her grubun ikişerli karşılaştırmaları yapılmış ve bu karşılaştırılan grupların ortalamaları arasındaki farklar(Mean Difference) sayısal olarak verilmiştir. Bu sayısal değerlerin yanında bir yıldız (*) işaretinin bulunması bu ikilinin ortalamaları arasında anlamlı bir farklılık olduğunu göstermektedir. Tablo incelendiğinde 1-4, 2-4 ve 3-4 ikililerinin yanında bir yıldız(*) işareti olduğu görülür. Yani bu ikililerin ortalamaları arasında anlamlı bir farklılık vardır.

Son olarak "Descriptive" tablosu incelendiğinde 4. grubun ortalamasının diğer gruplardan daha büyük olduğu görülür. Yani 4. ürün çeşidin satış miktarının, diğer grupların satış miktarlarından daha fazla olduğu söylenebilir.